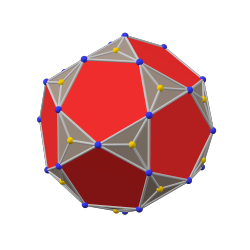
Chamfer (geometry)
This article needs additional citations for verification. (March 2025) |
In geometry, a chamfer or edge-truncation is a topological operator that modifies one polyhedron into another. It separates the faces by reducing them, and adds a new face between each two adjacent faces (moving the vertices inward). Oppositely, similar to expansion, it moves the faces apart outward, and adds a new face between each two adjacent faces; but contrary to expansion, it maintains the original vertices.
For a polyhedron, this operation adds a new hexagonal face in place of each original edge.
In Conway polyhedron notation, chamfering is represented by the letter "c". A polyhedron with e edges will have a chamfered form containing 2e new vertices, 3e new edges, and e new hexagonal faces.
Platonic solids
[edit]Chamfers of five Platonic solids are described in detail below.

- chamfered tetrahedron or alternated truncated cube: from a regular tetrahedron, this replaces its six edges with congruent flattened hexagons; or alternately truncating a cube, replacing four of its eight vertices with congruent equilateral-triangle faces. This is an example of Goldberg polyhedron GPIII(2,0) or {3+,3}2,0, containing triangular and hexagonal faces. Its dual is the alternate-triakis tetratetrahedron.[2]
- chamfered cube: from a cube, the resulting polyhedron has twelve hexagonal and six square centrally symmetric faces, a zonohedron.[3] This is also an example of the Goldberg polyhedron GPIV(2,0) or {4+,3}2,0. Its dual is the tetrakis cuboctahedron. A twisty puzzle of the DaYan Gem 7 is the shape of a chamfered cube.[4]
- chamfered octahedron or tritruncated rhombic dodecahedron: from a regular octahedron by chamfering,[5] or by truncating the eight order-3 vertices of the rhombic dodecahedron, which become congruent equilateral triangles, and the original twelve rhombic faces become congruent flattened hexagons. It is a Goldberg polyhedron GPV(2,0) or {5+,3}2,0. Its dual is triakis cuboctahedron.[2]
- chamfered dodecahedron: by chamfering a regular dodecahedron, the resulting polyhedron has 80 vertices, 120 edges, and 42 faces: 12 congruent regular pentagons and 30 congruent flattened hexagons. GPV(2,0) = {5+,3}2,0. The structure resembles C60 fullerene.[6] Its dual is the pentakis icosidodecahedron.[2]
- chamfered icosahedron or tritruncated rhombic triacontahedron: by chamfering a regular icosahedron, or truncating the twenty order-3 vertices of the rhombic triacontahedron. The hexagonal faces of the cI can be made equilateral, but not regular, with a certain depth of truncation. Its dual is the triakis icosidodecahedron.[2]
Regular tilings
[edit] Square tiling, Q {4,4} |
 Triangular tiling, Δ {3,6} |
 Hexagonal tiling, H {6,3} |
 Rhombille, daH dr{6,3} |

|

|

|

|
| cQ | cΔ | cH | cdaH |
Relation to Goldberg polyhedra
[edit]The chamfer operation applied in series creates progressively larger polyhedra with new faces, hexagonal, replacing the edges of the current one. The chamfer operator transforms GP(m,n) to GP(2m,2n).
A regular polyhedron, GP(1,0), creates a Goldberg polyhedra sequence: GP(1,0), GP(2,0), GP(4,0), GP(8,0), GP(16,0)...
| GP(1,0) | GP(2,0) | GP(4,0) | GP(8,0) | GP(16,0) | ... | |
|---|---|---|---|---|---|---|
| GPIV {4+,3} |
 C |
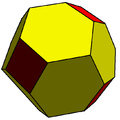 cC |
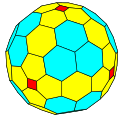 ccC |
 cccC |
ccccC |
... |
| GPV {5+,3} |
 D |
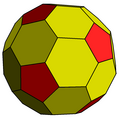 cD |
 ccD |
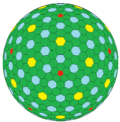 cccD |
 ccccD |
... |
| GPVI {6+,3} |
 H |
 cH |
 ccH |
cccH |
ccccH |
... |
The truncated octahedron or truncated icosahedron, GP(1,1), creates a Goldberg sequence: GP(1,1), GP(2,2), GP(4,4), GP(8,8)...
| GP(1,1) | GP(2,2) | GP(4,4) | ... | |
|---|---|---|---|---|
| GPIV {4+,3} |
 tO |
 ctO |
 cctO |
... |
| GPV {5+,3} |
 tI |
 ctI |
 cctI |
... |
| GPVI {6+,3} |
 tΔ |
 ctΔ |
cctΔ |
... |
A truncated tetrakis hexahedron or pentakis dodecahedron, GP(3,0), creates a Goldberg sequence: GP(3,0), GP(6,0), GP(12,0)...
| GP(3,0) | GP(6,0) | GP(12,0) | ... | |
|---|---|---|---|---|
| GPIV {4+,3} |
 tkC |
 ctkC |
cctkC |
... |
| GPV {5+,3} |
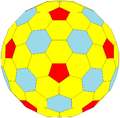 tkD |
 ctkD |
cctkD |
... |
| GPVI {6+,3} |
 tkH |
 ctkH |
cctkH |
... |
See also
[edit]References
[edit]- ^ Spencer 1911, p. 575, or p. 597 on Wikisource, Crystallography, 1. Cubic System, Tetrahedral Class, Figs. 30 & 31.
- ^ a b c d Deza, Deza & Grishukhin 1998, 3.4.3. Edge truncations.
- ^ Gelişgen & Yavuz 2019b, Chamfered Cube Metric and Some Properties.
- ^ "TwistyPuzzles.com > Museum > Show Museum Item". twistypuzzles.com. Retrieved 2025-02-09.
- ^ Gelişgen & Yavuz 2019b, Chamfered Octahedron Metric and Some Properties.
- ^ Gelişgen & Yavuz 2019a.
Sources
[edit]- Goldberg, Michael (1937). "A class of multi-symmetric polyhedra". Tohoku Mathematical Journal. 43: 104–108.
- Joseph D. Clinton, Clinton’s Equal Central Angle Conjecture [1]
- Hart, George (2012). "Goldberg Polyhedra". In Senechal, Marjorie (ed.). Shaping Space (2nd ed.). Springer. pp. 125–138. doi:10.1007/978-0-387-92714-5_9. ISBN 978-0-387-92713-8.
- Hart, George (June 18, 2013). "Mathematical Impressions: Goldberg Polyhedra". Simons Science News.
- Deza, A.; Deza, M.; Grishukhin, V. (1998). "Fullerenes and coordination polyhedra versus half-cube embeddings". Discrete Mathematics. 192 (1): 41–80. doi:10.1016/S0012-365X(98)00065-X..
- Gelişgen, Özcan; Yavuz, Serhat (2019a). "A Note About Isometry Groups of Chamfered Dodecahedron and Chamfered Icosahedron Spaces" (PDF). International Journal of Geometry. 8 (2): 33–45.
- Gelişgen, Özcan; Yavuz, Serhat (2019b). "Isometry Groups of Chamfered Cube and Chamfered Octahedron Spaces". Mathematical Sciences and Applications E-Notes. 7 (2): 174–182. doi:10.36753/mathenot.542272.
- Spencer, Leonard James (1911). . In Chisholm, Hugh (ed.). Encyclopædia Britannica. Vol. 07 (11th ed.). Cambridge University Press. pp. 569–591.
External links
[edit]- Chamfered Tetrahedron
- Chamfered Solids
- Vertex- and edge-truncation of the Platonic and Archimedean solids leading to vertex-transitive polyhedra Livio Zefiro
- VRML polyhedral generator (Conway polyhedron notation)
- VRML model Chamfered cube
- 3.2.7. Systematic numbering for (C80-Ih) [5,6] fullerene
- Fullerene C80
- How to make a chamfered cube